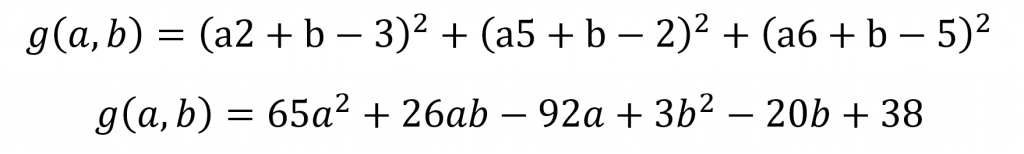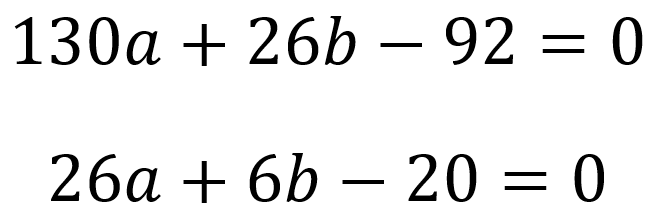Me, Hightech and I – Wie funktionieren eigentlich Neuronale Netze?
Was ist "künstliche Intelligenz"?
Geschätzte Lesezeit: 5 Minuten
 ElisaRiva | Pixabay
ElisaRiva | PixabayDie Fortschritte und Erstaunlichkeiten, die in den neuesten Entwicklungen zu sehen sind, wirken oftmals wie schwarze Magie: Ob es sich nun um Artikel über die brandneuen Roboter von Boston Dynamics oder selbstlernende Chatbots handelt, eines haben die Kommentare unter den KI-Beiträgen gemein: Weltuntergangszenarien und Vernichtung durch Terminatoren sind in diesen Diskussionen immer wieder zu entdecken.
Ob es hierbei um Sarkasmus und Belächelung der Technologie oder ernstgemeinte Bedenken geht, ist oft nicht erkennbar. Klar ist aber, dass beides in der Regel auf Unverständnis des Beobachters fußt. Der Mensch hat entweder Angst vor Dingen, die er nicht versteht, oder er verlacht sie, sofern sie einen scheinbar marginalen Einfluss auf sein Leben haben. Dass uns machine learning überall im virtuellen Alltag umgibt, ist allerdings heute schon Realität. Schrifterkennung auf dem Tablet, Gesichtserkennung in einem Foto, Instagramm Filter, individuelle Werbung auf Facebook, Optimierung von Filmmaterial auf Netflix, hochgenaue Erkennung tödlicher Krankheiten im frühsten Stadium… Die Anzahl der Beispiele ist unbegrenzt und jeder sollte eine Idee von der Funktionsweise der Technik haben. Deswegen geht es im Folgenden nicht etwa um eine philosophische Definition, ab wann und wie genau etwas als intelligent und künstlich angesehen werden kann. Auch geht es nicht um Vorzüge oder Risiken von maschinellem Lernen, sondern um grundlegende Ansätze und Funktionsweisen der Prinzipien dahinter. Vor etwas Oberstufenmathematik sollte man sich nicht scheuen.
Das Erste, das man mit Intelligenz in Verbindung bringt, ist das menschliche Gehirn als Zentrum unserer kognitiv analytischen Fähigkeiten. Übergeht man all die komplizierten Unterteilungen in Regionen bzw. Aufgabenbereiche des Gehirns, stößt man unausweichlich auf das Neuron als Grundbaustein. Das Neuron besteht aus einem Zellkörper, der Informationen sammelt, den Dentriten, die Informationen von benachbarten Neuronen zum Zellkörper leiten und dem Axon, das von dem Zellkörper Informationen an andere Neuronen weiterleitet. Ein Zellkörper kann entweder feuern, wenn ein gewisser Grenzwert von der Summe aller einkommenden Signale überschritten wird, oder es passiert eben nichts, wenn der Grenzwert nicht überschritten wird. Dies ist der stark vereinfachte Prozess, der in einem großen Netzwerk zwischen diesen Zellen abläuft.
Der Softwareingenieur, der eine künstliche Intelligenz erschaffen will, stellt sich nun die Frage: Was kann ich aus der Arbeitsweise dieses Grundbausteins lernen? Wie kann ich eine Datenstruktur erschaffen, die über ein ähnliches Verhalten wie ein Gehirn verfügt, die ich jedoch mit bekannten Verfahren manipulieren kann? Das Künstliche Neuronale Netz (KNN) ist erfunden.
Die ersten Gedanken und Arbeiten bezüglich Künstlicher Neuronaler Netze (KNN) finden sich erstaunlicherweise schon in den 1940er Jahren. Das sogenannte McCulloch-Pitts-Neuron von 1943 ist eines der ersten Modelle, die nach dem oben erklärten vereinfachtem Modell funktionieren. Ein Modell von Nervenzellen zu haben, ist zwar die Grundlage, aber wie kriegt man ein allgemeines Modell dazu, mir die Ergebnisse zu liefern, die ich benötige? Wie schafft man es, das neuronale Netz zu trainieren? Der erste Gedanke ist, dass man Trainingsbeispiele braucht. Wenn ich beispielsweise ein Bild von einer Linkskurve in das Netz eines autonomen Fahrzeugs gebe, möchte ich sehen, dass es ausgibt, nach links zu lenken. Gibt es stattdessen aus „lenke nach rechts“, weiß ich, dass etwas am Netz verändert werden muss. Dieses Training wird mit mehreren Millionen Beispielen wiederholt, bis das Netz mit an Sicherheit grenzender Wahrscheinlichkeit seine Aufgabe erfüllt. An dem Aachener Forschungsinstitut für Bildverarbeitung werden beispielsweise medizinische Bilder von Organen durch neuronale Netze in der Art ausgewertet, dass es gelingt, Krebszellen im frühsten Stadium mit einer Zuverlässigkeit aufzuspüren, die selbst ein Experte nicht überbieten kann.
Wie genau hat man sich ein solches Training vorzustellen?
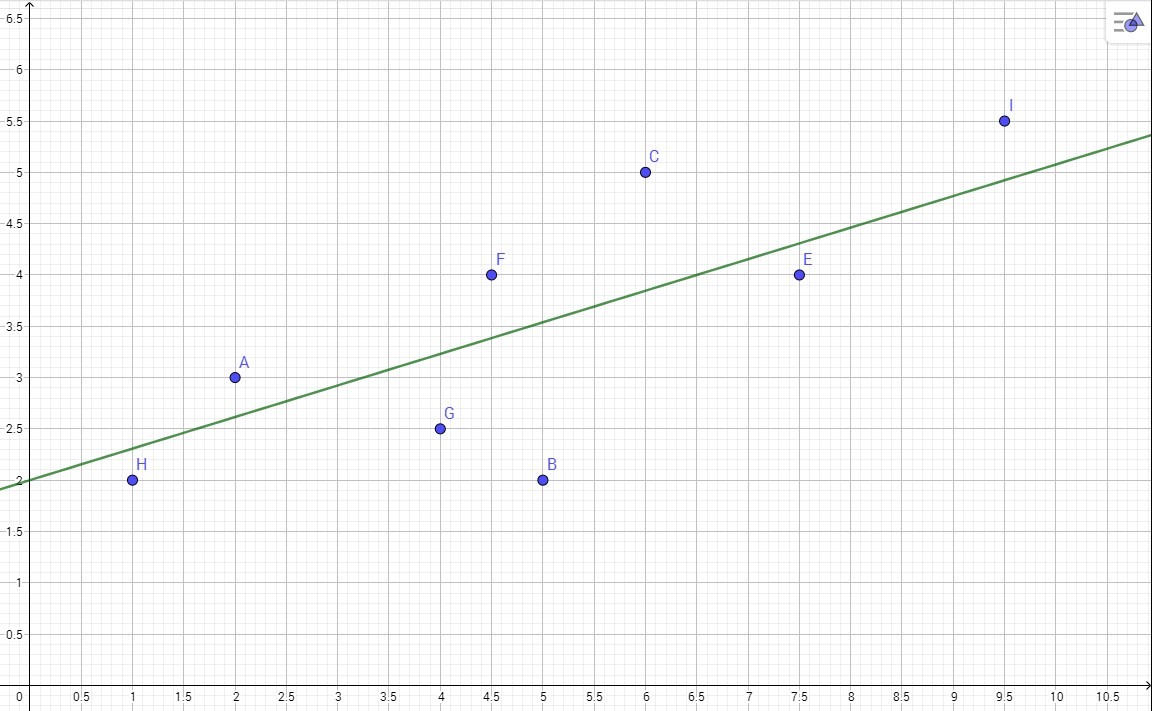
Man kann ein neuronales Netz als Abbildung sehen: Man gibt Daten herein und andere Daten kommen heraus. Denkt man nun in Richtung Matheunterricht, fällt einem sofort das Stichwort „Funktion“ ein. Man setzt z.B. eine 2 in f(x)=5x+4 herein und die 14 kommt heraus. f(x)=5x+4 fungiert jetzt als extrem einfaches neuronales Netz. Da wir es nicht trainiert haben, wissen wir zunächst nicht, wie genau es definiert ist. Also statt f(x)=5x+4 erhalten wir das allgemeine Modell f(x)=ax+b. Aufgabe des Trainings ist es nun, die besten a und b auf Grundlage von Trainingsdaten herauszufinden. Ein Trainingsdatensatz besteht aus einem x, das ins neuronale Netz eingegeben wird und aus einem erwarteten Ergebnis y. Es handelt sich also um Punkte in der x, y Ebene. Sagen wir, wir haben folgende Daten (wie genau die Linie verläuft, gilt es herrauszufinden):
(2, 3)(1, 2)(5, 2)(6, 5)(4, 2.5)(4.5, 4)(7.5, 4)(9.5, 5.5)
(2,3),(5,2) und (6,5) verwenden wir zum Trainieren, den Rest verwenden wir zum Testen, ob das Netz funktioniert. Ziel ist es in erster Linie, dass f(x) möglichst genau unsere Trainingsdaten trifft, anschließend wird verglichen, ob das Ergebnis auch zu den unbekannten Testdaten passt.
Es muss also die Summe der quadratischen Fehler minimiert werden:
Dann setzt man die Ableitungen der konvexen Funktion gleich Null:
Als Lösung des Gleichungssystems ergibt sich a = 4/13 und b = 2 bei einem Gesamtfehler von 50/13.
Das trainierte Neuronale Netz wird also durch f(x)= 4/13 x + 2 beschrieben. Mit den übrigen Testdaten kann nun verglichen werden, wie gut das Modell funktioniert. Nun kann man Ergebnisse für beliebige Eingaben vorhersagen, indem man das Ergebnis 4/13 x + 2 für verschiedene x berechnet.
Die vorgeführte Rechnung beschreibt ein neuronales Netz, das aus genau zwei linearen Neuronen besteht. Einem sogenannten Bias-Neuron, das kontinuierlich mit dem Wert 2 feuert und einem normalen Neuron. Dies ist eines der einfachst möglichen neuronalen Netze (auch lineare Regression genannt).
Wie sieht die Arbeit in der Praxis aus?
Die künstlichen Netze, die für reale Anwendungen verwendet werden, verfügen oft über viele tausend Neuronen (kleinstes Insekten Gehirn ~100000 Neuronen), die in mehrere Stufen hintereinander gestaffelt sind, und zudem über eine sogenannte nichtlineare Aktivierungsfunktion verfügen. Nun gilt es, in einem bis zu Milliarden-dimensionalen Vektorraum, das Minimum einer hochgradig nichtlinearen Abbildung zu finden. (In obigem Beispiel wurden in einem 2d-Vektorraum das Minimum einer linearen Abbildung gefunden.) Dieses Minimum ist die optimale Lösung der Aufgabe.
Der Umgang und die Optimierung solcher Netze auf verschiedenste Probleme ist das, womit sich Forscher, Ingenieure, Informatiker und Mathematiker beschäftigen. Dies ist in den allermeisten Fällen gemeint, wenn der Volksmund von künstlicher Intelligenz spricht. Um es nochmal deutlich zu machen: die obige Rechnung ist eine sehr starke Vereinfachung des realen Konzeptes.
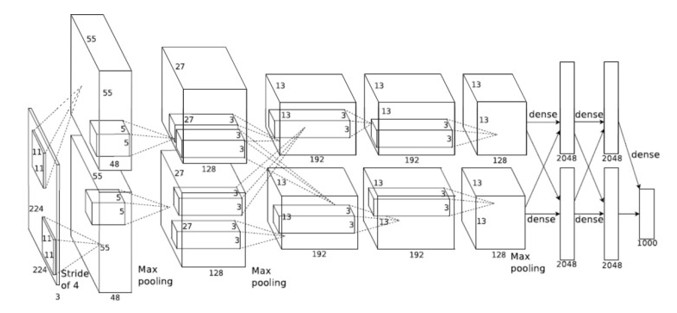
Hier abgebildet sieht man ein typisches Layout des Convolutional Neural Networks Alexnet, das 2012 mit einem Preis für die hochgenaue Klassifizierung von Objekten ausgezeichnet wurde.
Angesichts der gigantischen Komplexität, die ein solches System bietet, lässt sich erahnen, wie es sein kann, dass sich ein Konstrukt wie der Mensch Gedanken über dieses Thema machen kann.
Unterstützen
Wenn dir der Beitrag gefallen hat, würden wir uns über eine kleine Spende freuen.
Noch mehr Stories? Folge seitenwaelzer:
Benedikt Buller
Ich bin Benedikt Buller und Student der Elektrotechnik, Informationstechnik und technischen Informatik an der RWTH Aachen. Neben dem Studium bin ich Ingenieur beim Ecurie Formula Student Team in der Gruppe "autonomes Fahren".
 Daniel Öberg | Unsplash
Daniel Öberg | Unsplash Korallen, Klimawandel und Klimaangst
 Students for Future Germany
Students for Future Germany Die Public Climate School – Vom Hochschulstreik zum Verein Klimabildung e.V.
 Jiroe Matia Rengel | Unsplash
Jiroe Matia Rengel | Unsplash Queerness im Meer
 Midjourney
Midjourney Wer sagt hier eigentlich was? Künstliche Intelligenz und die Zukunft des Schreibens
Tags: AiBig DataBilderkennungConvolutional Neural Networkdeep learningInformatikKIkünstliche IntelligenzMathematikneuronale NetzeRoboterSpracherkennung